엘리어트 파동이론의 배경 및 정의, 엘리어트 파동이론의 법칙 그리고 엘리어트 파동이론의 근간이 되는 피보나치수열과 황금비율에 대해서 알아보는 시간을 갖도록 하겠습니다.
엘리어트 파동이론은 지수나 주가의 움직임을 파동 법칙에 의거한 기술적 분석 도구로 많은 분들이 사용하고 있고, 특히 주가의 패턴, 주가의 지지선과 저항선 그리고 주가의 추세 등과 연계하여 보다 강력한 분석 도구로 활용할 수 있습니다.
엘리어트 파동이론은 개인마다 그 활용도에 따라 또는 각자의 해석에 따라 많은 차이와 견해를 보이는 것은 사실이지만, 오늘은 엘리어트 파동이론이 갖는 특징과 엘리어트 파동이론이란 무엇인지 쉽게 접근하여 이해할 수 있는 수준으로 이 글을 시작하려고 합니다.
엘리어트 파동이론의 배경
엘리어트 파동이론은 회계사이자 주식 분석가 랠프 넬슨 엘리어트(Ralph Nelson Elliott)가 1938년 발표한 파동이론 'The Principle of Wave'라는 저서를 통해 알려지게 되었습니다.
그는 75년간의 분량 데이터를 분간, 일간, 주간, 월간, 년간 등으로 꼼꼼히 분석하여 주가 움직임에 숨겨진 법칙을 찾고자 하였으며, 예측 불가능하고 무질서 상태인 것처럼 보였던 추세가 실제로는 자연의 법칙과 우주 만물의 현상과 일치한다는 것이 이 엘리어트 파동이론의 근간이 되게 됩니다.
엘리어트 파동이론은 1935년 미국 증시 대폭락을 예측했었고, 이후 이론적 신봉자였던 프레히터가 1987년 10월 19일 월요일 뉴욕증권시장의 주가가 대폭락 하는 블랙 먼데이(Black Monday)를 정확하게 예언해 당시 많은 주목을 받기도 하였습니다.
엘리어트 파동이론의 탄생 및 정의 그리고 한계점
엘리어트 파동 이론은 5개의 상승 파동과 3개의 하락 파동으로 구성된 총 8개의 파동이 하나의 사이클을 형성하며, 엘리어트는 주가의 추세가 자연물 중 하나인 '파동'과 비슷하고 실제로는 자연의 법칙을 따르며, 피보나치수열 안에서 예측 가능한 것으로 정의하였습니다.
엘리어트 파동이론이 발표되고 처음에는 어느정도 이목이 집중되었으나 시간이 지날수록 불규칙적인 주식 시장 환경에 많은 오류와 한계에 부딪히게 되고, 특히 파동의 시작과 끝이 명확하지 않고 파동이 나타나는 시간적 개념의 부재에 따른 단점들을 노출하게 되면서 그 인기도 사라지게 되었습니다.
엘리어트 파동이론에 대해서 많은 사람들이 여전히 갑론을박 상황이지만 지수의 기술적 분석 도구로써 충분한 가치가 있는 유용한 지표라고 생각합니다.
엘리어트 파동이론의 기초 및 개념
엘리어트 파동이론의 기초이자 가장 근본이 되는 패턴, 피보나치 수열과 비율 그리고 자연의 법칙에 대한 개념을 하나씩 알아 보면서, 왜 엘리어트 파동이론에서 이를 중요시 하고 있는지 살펴 보도록 하겠습니다.
1. 엘리어트 파동 패턴(Pattern)
엘리어트 파동이론에 비춰 볼 때 패턴이라 함은 그 시작이 N자형 파동 형태에 가깝고, 이때 N자형 패턴이 연속되면서 헤드 앤 숄더 패턴과 역헤드 앤 숄더 패턴으로 확장되는 가장 이상적인 패턴 모델로 피보나치 파동 법칙을 설명하고 이해하는데 많은 도움이 될 수 있을 것으로 기대해 봅니다.
2. 피보나치수열과 비율 그리고 황금비율
엘리어트 파동이론의 가장 기본이 되는 피보나치 수열과 비율 그리고 황금비율에 대한 정의는 다음과 같습니다.
2-1. 피보나치 수열과 비율
엘리어트 파동이론에서 말하는 피보나치수열은 나열된 자연수의 두 수의 합이 바로 뒤의 수가 되는 배열 형태로 처음 시작하는 두 항은 1이고, 셋째 항부터는 두 인접한 항을 더한 합을 그 바로 다음 항으로 정의합니다.
따라서 피보나치수열을 예제를 통해 나열해 보면 첫 번째 항과 두 번째 항은 각각 1로 시작한다고 하였고 그리고 두 인접 항을 더한 합의 수열로 나열해 보면 다음과 같은 수열이 나오게 됩니다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 순으로 수열이 나열되게 됩니다.
이렇게 나열되는 수열이 바로 엘리어트 파동이론의 근간이 되는 피보나치 수열이 되겠습니다.
2-2. 피보나치 비율
피보나치 비율은 나열된 피보나치수열을 이용하여 앞 수를 뒷 수로 나누거나 또는 뒷 수를 앞 수에 나누어 보면 그 비율은 다음과 같습니다.
위 피보나치 수열을 이용하여 각각 그 비율을 나누어 보겠습니다.
앞 수(21) / 뒷 수(34) = 0.618
뒷 수(55) / 앞 수(34) = 1.618
앞 수(21) / 뒷 수(55) = 0.382
이렇게 앞 수와 뒷 수, 뒷 수와 앞 수를 나누어 보면 그 비율이 0.382, 0.618, 1.618 비율에 값들이 각각 수렴한다는 사실을 알 수 있습니다.
2-3. 황금비율
황금비율은 1:1.618의 비율을 이르는 말로 자연수로 바꾸면 3:5 또는 5:8에 가까운 비율로, 모든 요소가 조화 및 대칭을 이루어 보기에 편안하고 아름답게 느껴지는 비율로 이를 황금 비율이라고 합니다.
우연의 일치 일지는 모르지만 이 황금비율과 엘리어트 파동이론의 근간이 되는 피보나치수열은 일맥 상통하는 부분이 있습니다.
황금비율의 사례로 소라나 고동의 나선 모양, 식물 잎의 수나 가지 수, 레오나르도 다빈치의 인체 비례도, 이집트 피라미드 구조, 태풍과 은하수의 모양, 파도, 8등신 그리고 엘리어트 파동이론에서 말하는 3파동과 5파동 등 이 모두가 황금비율에 기인한 것으로 일상, 자연, 인체, 주식시장 등 모든 만물은 일정한 자연의 법칙에 따라 일정한 패턴을 가질 수 밖에 없다는 것입니다.
2-4. 자연의 법칙
엘리어트 파동이론에서 말하는 자연의 법칙은 앞에서도 말씀을 드렸지만 예측 불가능하고 무질서 상태인 것처럼 보이지만 실제로는 모든 만물들은 일정한 자연의 법칙을 따른다는 것입니다.
우리는 지금까지 엘리어트 파동이론의 근간이 되는 엘리어트 파동이론의 배경, 엘리어트 파동의 패턴, 피보나치 수열과 비율, 황금비율, 자연의 법칙 등에 대해서 간략하게 알아 보았습니다.
그러면 본격적으로 엘리어트 파동이론에 대해서 알아 보도록 하겠습니다.
엘리어트 파동이론
엘리어트 파동은 추세의 연장선상에서 끊임없이 반복하며 , 각각의 파동은 아래 그림처럼 일정한 패턴 또는 사이클로 이루어진다는 이론입니다.
그러면 엘리어트 파동이론 그림을 보시면서 하나씩 설명을 드려 보겠습니다.
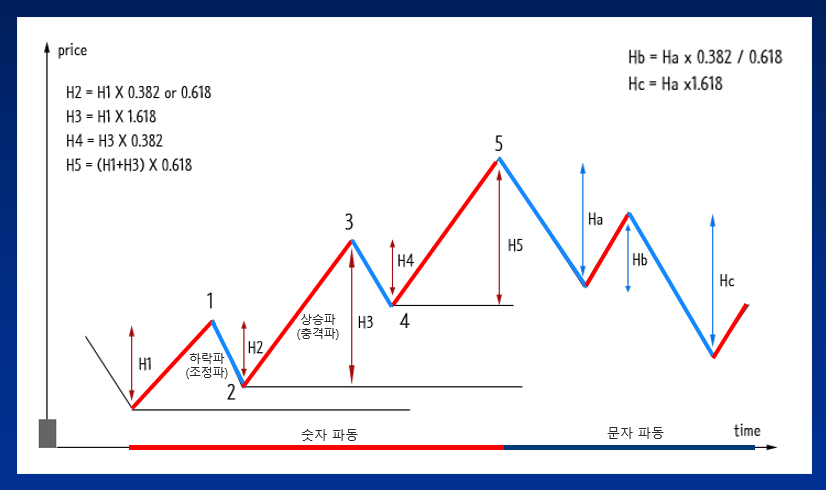
엘리어트 파동이론의 구성
엘리어트 파동이론은 크게 숫자 파동인 상승 파동과 문자 파동인 하락 파동으로 구분되고, 숫자 파동인 상승 파동은 총 5개의 파동이 형성되며, 문자 파동인 하락 파동은 총 3개의 파동으로 구성되어 총 8개의 파동으로 구성되어집니다.
엘리어트 파동이론의 상승 파동 (숫자 파동)
엘리어트 파동이론에서 상승 파동은 숫자 파동으로 총 5개의 파동으로 구성되어지며, 이 5개의 파동 중에서 1 파동, 3 파동, 5 파동은 상승파 또는 충격파(Impulse Wave)라고 합니다. 이 3개의 상승 파동은 추세의 방향과 일치하며 해당 파동 추세 안에는 또 다른 5개의 작은 파동들이 만들어집니다.
이와 반대로 5개의 파동 중에서 2 파동, 4 파동은 하락파 또는 조정파(Corrective Wave)라고 하는데, 이 2개의 하락 파동은 추세의 반대 방향으로 해당 파동 추세 안에는 또 다른 3개의 작은 파동들이 만들어집니다.
엘리어트 파동이론의 하락 파동 (문자 파동)
엘리어트 파동이론에서 하락 파동은 문자 파동으로 총 3개의 파동으로 구성되어지며, 이 3개의 파동을 a파동, b파동, c파동이라고 부릅니다.
숫자 파동에서와 마찬가지로 문자 파동인 a파동, b파동, c파동 또한 추세의 같은 방향인 a파동, c파동은 추세의 정방향으로 해당 파동 추세 안에는 또 다른 5개의 작은 파동들이 만들어지고, 이와 반대로 b파동은 하락 추세의 반대 방향으로 인해 추세 안에는 또 다른 3개의 작은 파동들이 만들어집니다.
엘리어트 파동이론 차트의 이해
엘리어트 파동이론에서 말하는 총 8개의 파동 중 첫 번째 파동을 1 파동이라 하고 상승 파동인 1파동 안에는 또 다른 5개의 작은 파동들로 구성되며, N자형 상승 파동의 기초가 되기도 합니다.
엘리어트 파동이론 1 파동
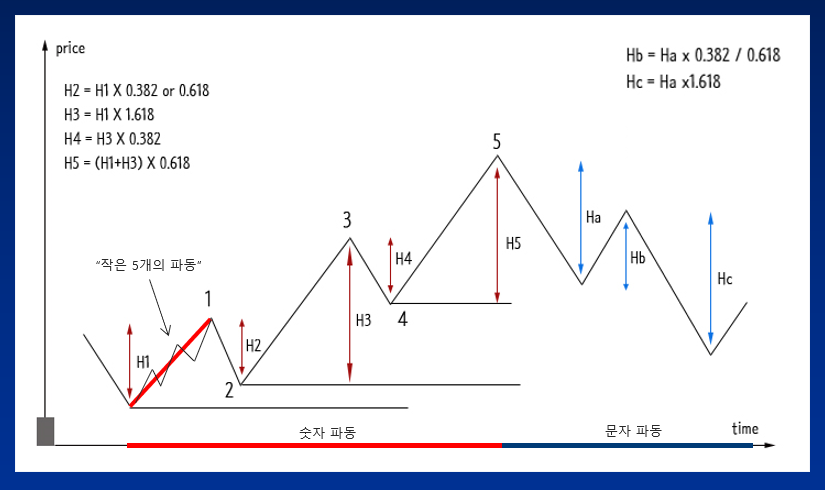
엘리어트 파동의 1파동은 추세가 상승으로 전환하는 강력한 신호이기 때문에 이전 추세가 하락 추세에서 상승 추세로 전환이 되는 초기 구간인지 또는 상승 추세에서 또 다른 상승 추세 국면으로 이어지는 추세인지에 따라서 수익도 극대화 할 수 있는 전략을 세울 수 있는 파동 구간이 되겠습니다.
엘리어트 파동이론 2 파동
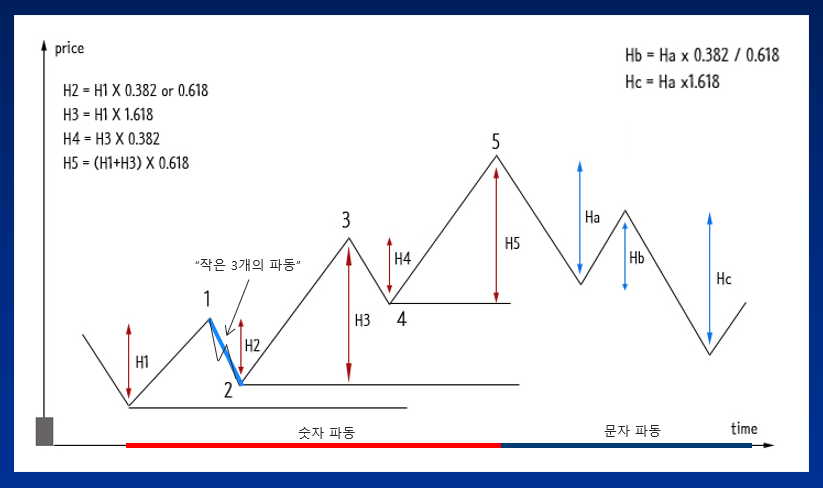
엘리어트 파동의 2 파동은 하락파 또는 조정파로 되돌림 구간이 나오는 파동으로 추세의 역방향이기 때문에 또 다른 작은 3개의 파동이 존재합니다.
2 파동 H2는 첫 번째 1파동의 시작점인 저점 보다 낮을 수 없으며, 일반적으로 2파동 H2는 H1의 0.382 or 0.618배의 지점에서 반등을 시도하는 것이 안정된 파동의 변곡점이 됩니다.
엘리어트 파동이론 3 파동
3 파동(H3)은 1 파동의 높이 값(H1) X 1.618배 가격까지 상승하는 것이 일반적이며, 최적의 안정된 파동이 됩니다.
엘리어트 파동이론 4 파동
4 파동(H4)은 조정파 또는 되돌림 구간으로 3 파동의 저점 가격보다 낮아질 수 없으며, 그 조정의 깊이는 H3 X 0.382배까지 하락하다가 되돌리는 게 일반적입니다.
엘리어트 파동이론 5 파동
숫자 파동의 마지막 상승 파동인 엘리어트 파동 5파동 H5는 H1+H3를 더한 높이 X 0.618배 까지 상승하는 것이 일반적이며, 이로써 상승 파동이 마무리되고 추세가 꺾이면서 하락 추세로 전환이 됩니다.
엘리어트 파동이론 a파동
엘리어트 파동이론에서 말하는 하락 파동인 문자 파동은 총 3개의 파동으로 구성되며 a파동, b파동, c파동이라고 합니다.
먼저 a파동을 살펴보면 a파동은 5 파동 상승 파동이 일어나고 난 이후 첫 번째 하락 추세로 전환이 되는 파동 구간으로 충격이 커지는 파동 구간이 되겠습니다.
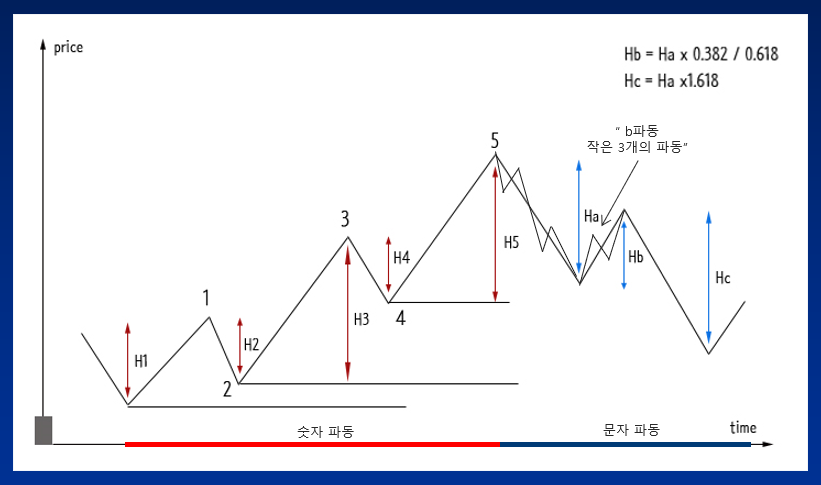
a파동은 하락 추세의 하락 파동 구간으로 총 5개의 소 파동이 만들어지는 구간으로, 일반적으로 고점 징후 형태인 쌍곡점 또는 삼산봉(쓰리 고점)이 만들어진 이후 급락하는 패턴들의 모습이 일반적 사례입니다.
엘리어트 파동이론 b파동
엘리어트 파동이론 b파동은 하락 a파의 고점을 b파가 훼손할 수 없으며, 그 높이는 Hb는 Ha X 0.382(0.618) 배까지 상승하는 것이 일반적입니다.
해당 하락 파동 구간을 상승 파동 구간으로 오인할 수 있는 구간이 되기 때문에 주의가 필요한 구간이 되겠습니다.
엘리어트 파동이론 c파동
엘리어트 파동이론 c파동은 하락 3파동으로 Hc는 Hb X 1.618배 까지 하락하고 나서 새로운 파동이 시작되는 구간이 되겠습니다.
하지만 c파동이 계속 하락 추세의 연장선상이 될 수도 있기 때문에 해당 파동 구간에서 모든 파동이 소실된다고 하여 추세의 파동이 하락 추세로 계속 이어지지 않을 것이란 보장은 없기 때문에 주의도 필요합니다.
엘리어트 파동이론의 단점
끊임없는 반복된 파동은 존재할지라도 주가의 움직임이 엘리어트 파동이론에서 말하는 8개의 파동 원리로만 움직이는 것은 아니며, 또한 의미 있는 파동이 항상 일어나는 것도 아니기 때문에 시간적 제약에 대한 단점이 있을 수 있습니다.
하지만 투자자들이 이를 응용하고 접목하는 차원에서는 상당히 우수한 기술적 분석 도구 이기 때문에, 꼭 한번 정독하시면 좋지 않을까 하는 개인적 생각입니다.
특히 지지와 저항 그리고 돌파의 개념으로 엘리어트 파동이론을 접목하게 되면 강력한 분석도구가 될 수 있기 때문에 개인적으로 선호하는 기술적 분석도구 이기도 합니다.
오늘은 여기까지 엘리어트 파동이론에 대한 기본적인 개념에 대해 강의를 드렸습니다.
다음 시간에는 엘리어트 파동이론에 기반한 Zigzag Pattern, Flat Pattern, Irregular Pattern, Triangle Pattern 등 다양한 패턴들에서 엘리어트 파동이론을 어떻게 접목하여 활용하는지에 대해서 함께 살펴볼 수 있는 시간을 마련해 보도록 하겠습니다.
코멘트
엘리어트 파동이론과 관련하여 추가적인 의견이 있으시면, 언제든지 의견 남겨 주십시오.
'금융교육' 카테고리의 다른 글
| 주식 차트보는 법, 주식 차트 패턴 유형과 매매 기법 (55) | 2024.01.29 |
|---|---|
| ETF란 무엇이고, ETF 투자하는 방법은 무엇인가 (60) | 2024.01.23 |
| CCI 지표 개요와 해석 그리고 CCI 보조지표 보는 법 (29) | 2024.01.16 |
| 해외 선물과 선물 옵션, 선물 옵션 만기일 그리고 레버리지 뜻 (44) | 2024.01.14 |
| 현물 ETF와 선물 ETF의 차이와 투자 방법 (46) | 2024.01.12 |




댓글